Linear Discriminant Analysis
- 目标:处理两类线性判别问题
- 思想:对于两类的线性判别问题,可以看作是把所有样本都投影到某一个方向上,然后在沿着这个方向上的一维空间中确定一个分类的阈值,过这个阈值点且与投影方向垂直的超平面就是两类的分类面。
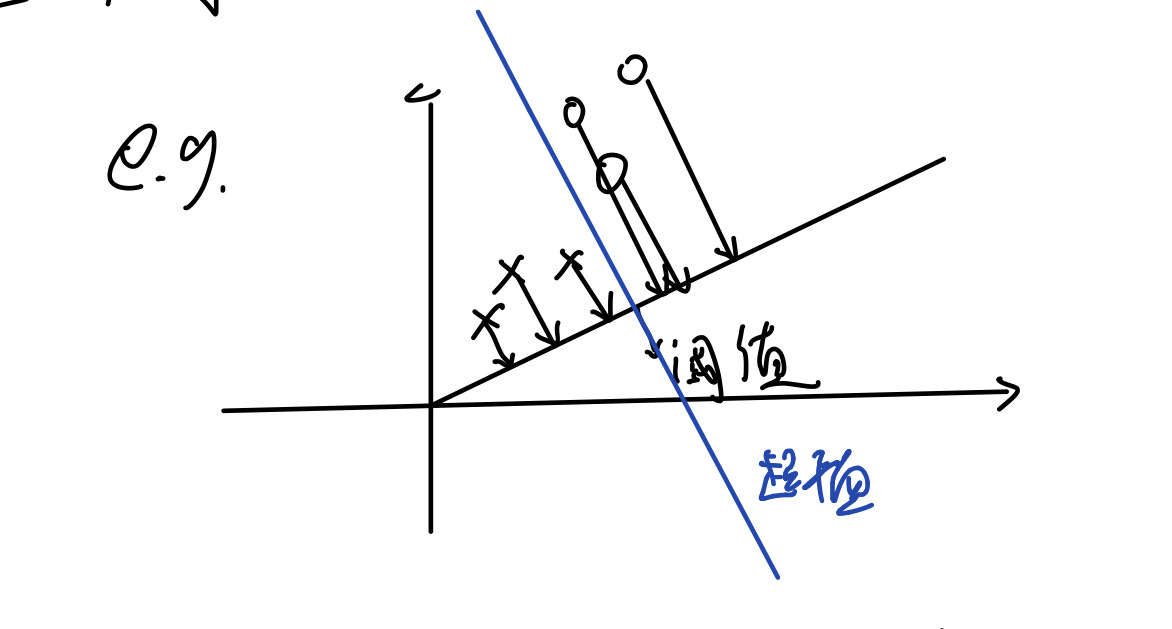
- 问题:如何找到这个超平面,=> 即如何确定投影方向?
背景描述:
设样本集为$\mathscr{X} = { \mathbf{x}{1}, \mathbf{x}{2}, … \mathbf{x}{n}}$, 其中$\mathbf{x}{i}$是d维向量, 代表一个样本,包含d个特征,属于某一类$\omega$
比如其中$\omega_{1}$类的样本集是$\mathscr{X}{1}={\mathbf{x}^1_1, \mathbf{x}^1_2, …, \mathbf{x}^1_n}$, $\omega{2}$类的样本集是$\mathscr{X}_{2}={\mathbf{x}^2_1, \mathbf{x}^2_2, …, \mathbf{x}^2_n}$
核心思想:将d维的样本投射到一维空间中,方便分类;
确定一个投影方向$\mathbf{w}$(d维向量), 使得$y_i=\mathbf{w}^T\mathbf{x}_i$, (1xd*dx1=1, $y_i$是一个值),这个式子是将样本$\mathbf{x}_i$投影到$\mathbf{w}$方向上。
对于第i类的样本空间:其均值向量为\(\mathbf{m}_i=\frac{1}{N_i} \sum\limits_{\mathbf{x}_j \in \mathscr{X}_i} \mathbf{x}_j\quad,\quad i=1, 2\)
$\mathbf{m}_i$是d维向量
\(\mathbf{m}_i=\frac{1}{N_i}\begin{pmatrix} \begin{pmatrix} x_{11} \\ x_{12} \\ \vdots \\ x_{1d} \end{pmatrix} + \begin{pmatrix} x_{21} \\ x_{22} \\ \vdots \\ x_{2d} \end{pmatrix} + \dots + \begin{pmatrix} x_{N_i1} \\ x_{N_i2} \\ \vdots \\ x_{N_id} \end{pmatrix} \end{pmatrix} = \begin{pmatrix} \mu_1 \\ \mu_2 \\ \vdots \\ \mu_d \end{pmatrix}\)
上式中每一列向量代表具有d个特征的第i类的一个样本。对于两类问题我们可以得到第一类的均值向量$\mathbf{m}_1$和第二类的均值向量$\mathbf{m}_2$
定义各类的类内离散度矩阵(within-class scatter matrix)为 \(\mathbf{S}_i=\sum\limits_{\mathbf{x}_j \in \mathscr{X}_i} (\mathbf{x}_j-\mathbf{m}_i)(\mathbf{x}_j-\mathbf{m}_i)^T, \quad i=1,2\) 其中$\mathbf{S}_i$是dxd的矩阵。